Kiểm tra dự phòng theo chu kỳ là tính toán một tập hợp các mã xác nhận dựa trên dữ liệu để kiểm tra xem dữ liệu có bị thay đổi hoặc truyền lỗi trong quá trình truyền dữ liệu hay không.

Nguyên lý thuật toán

Giả sử rằng thông tin nhị phân 15 bit g = 101001110100001 cần được gửi trong quá trình truyền dữ liệu, chuỗi mã nhị phân này có thể được biểu diễn dưới dạng đa thức đại số g (x) = x ^ 14 + x ^ 12 + x ^ 9 + x ^ 8 + x ^ 7 + x ^ 5 + 1, trong đó giá trị của bit thứ k tính bằng g tương ứng với hệ số của x ^ k tính bằng g (x). Nhân g (x) với x ^ m, thêm m số không sau g, rồi chia cho đa thức bậc m h (x) để thu được mã nhị phân r tương ứng với số hạng còn lại có thứ tự (m-1) r (x) Đó là mã hóa CRC.

h (x) có thể được lựa chọn tự do hoặc sử dụng các tiêu chuẩn được quốc tế chấp nhận. Nói chung, thuật toán CRC được gọi là CRC-m theo thứ tự m của h (x), chẳng hạn như CRC-32, CRC-64, v.v.

Phép chia g (x) và h (x) có thể được thực hiện bằng phép toán xor (OR) thông qua g và h. Ví dụ: thực hiện thao tác xor trên 11001 và 10101:

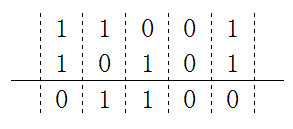
明白了xor运算法则后，举一个例子使用CRC-8算法求101001110100001的效验码。CRC-8标准的h(x) = x^8 + x^7 + x^6 + x^4 + x^2 + 1，既h是9位的二进制串111010101。

经过迭代运算后，最终得到的r是10001100，这就是CRC效验码。

通过示例，可以发现一些规律，依据这些规律调整算法： 

1. 每次迭代，根据gk的首位决定b，b是与gk进行运算的二进制码。若gk的首位是1，则b=h；若gk的首位是0，则b=0，或者跳过此次迭代，上面的例子中就是碰到0后直接跳到后面的非零位。

2. 每次迭代，gk的首位将会被移出，所以只需考虑第2位后计算即可。这样就可以舍弃h的首位，将b取h的后m位。比如CRC-8的h是111010101，b只需是11010101。 

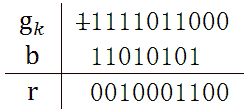
3. 每次迭代，受到影响的是gk的前m位，所以构建一个m位的寄存器S，此寄存器储存gk的前m位。每次迭代计算前先将S的首位抛弃，将寄存器左移一位，同时将g的后一位加入寄存器。若使用此种方法，计算步骤如下： 

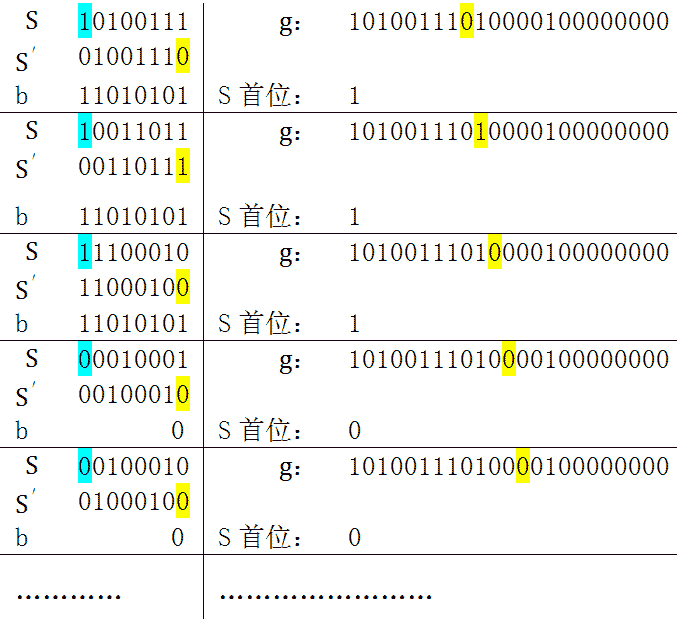
※蓝色表示寄存器S的首位，是需要移出的，b根据S的首位选择0或者h。黄色是需要移入寄存器的位。S'是经过位移后的S。

查表法

同样是上面的那个例子，将数据按每4位组成1个block，这样g就被分成6个block。

下面的表展示了4次迭代计算步骤，灰色背景的位是保存在寄存器中的。 

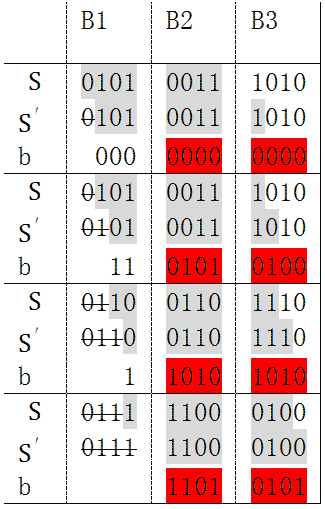
经4次迭代，B1被移出寄存器。被移出的部分，不我们关心的，我们关心的是这4次迭代对B2和B3产生了什么影响。注意表中红色的部分，先作如下定义：

   B23 = 00111010
   b1 = 00000000
   b2 = 01010100
   b3 = 10101010
   b4 = 11010101
   b' = b1 xor b2 xor b3 xor b4

4次迭代对B2和B3来说,实际上就是让它们与b1,b2,b3,b4做了xor计算，既：

   B23 xor b1 xor b2 xor b3 xor b4

可以证明xor运算满足交换律和结合律，于是：

   B23 xor b1 xor b2 xor b3 xor b4 = B23 xor (b1 xor b2 xor b3 xor b4) = B23 xor b'

b1是由B1的第1位决定的，b2是由B1迭代1次后的第2位决定（既是由B1的第1和第2位决定），同理,b3和b4都是由B1决定。通过B1就可以计算出b'。另外，B1由4位组成，其一共2^4有种可能值。于是我们就可以想到一种更快捷的算法，事先将b'所有可能的值，16个值可以看成一个表；这样就可以不必进行那4次迭代，而是用B1查表得到b'值，将B1移出，B3移入，与b'计算，然后是下一次迭代。

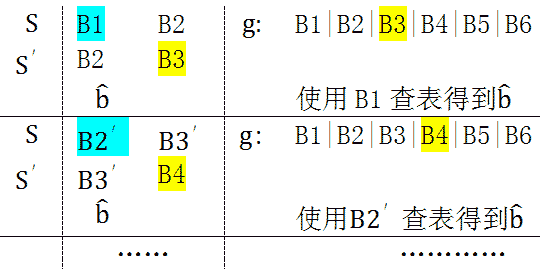
可看到每次迭代，寄存器中的数据以4位为单位移入和移出，关键是通过寄存器前4位查表获得
，这样的算法可以大大提高运算速度。

上面的方法是半字节查表法，另外还有单字节和双字节查表法，原理都是一样的——事先计算出2^8或2^16个b'的可能值，迭代中使用寄存器前8位或16位查表获得b'。
 

反向算法

之前讨论的算法可以称为正向CRC算法，意思是将g左边的位看作是高位，右边的位看作低位。G的右边加m个0，然后迭代计算是从高位开始，逐步将低位加入到寄存器中。在实际的数据传送过程中，是一边接收数据，一边计算CRC码，正向算法将新接收的数据看作低位。

逆向算法顾名思义就是将左边的数据看作低位，右边的数据看作高位。这样的话需要在g的左边加m个0，h也要逆向，例如正向CRC-16算法h=0x4c11db8，逆向CRC-16算法h=0xedb88320。b的选择0还是h，由寄存器中右边第1位决定，而不是左边第1位。寄存器仍旧是向左位移，就是说迭代变成从低位到高位。